Закон всемирного тяготения

Эксперимент Кавендиша

Эксперимент по определению точного значения гравитационной постоянной впервые предложил английский естествоиспытатель Джон Мичелл, который сконструировал крутильные весы. Однако, не успев провести эксперимент, в 1793-м году Джон Мичелл умер, а его установка перешла в руки Генри Кавендишу – британскому физику. Генри Кавендиш улучшил полученное устройство и провел опыты, результаты которых были опубликованы в 1798-м году в научном журнале под названием «Философские труды Королевского общества».

Генри Кавендиш (1731 — 1810)

Установка для проведения эксперимента состояла из нескольких элементов. Прежде всего она включала 1,8-метровое коромысло, к концам которого крепились свинцовые шарики с массой 775 г и диаметром 5 см. Коромысло было подвешено на медной 1-метровой нити. Несколько выше крепления нити, ровно над ее осью вращения устанавливалась еще одна поворотная штанга, к концам которой жестко крепились два шара массой 49,5 кг и диаметром 20 см. Центры всех четырех шаров должны были лежать в одной плоскости. В результате гравитационного взаимодействия притяжение малых шаров к большим должно быть заметно. При таком притяжении нить коромысла закручивается до некоторого момента, и ее сила упругости должна равняться силе тяготения шаров. Генри Кавендиш измерял силу тяготения посредством измерения угла отклонения плеча коромысла.

Установка Генри Кавендиша

Более наглядное описание эксперимента доступно в видео ниже:

Для получения точного значения константы Кавендишу пришлось прибегнуть к ряду мер, снижающих влияние сторонних физических факторов на точность эксперимента. В действительности Генри Кавендиша проводил эксперимент не для того, чтобы выяснить значение гравитационной постоянной, а для расчета средней плотности Земли. Для этого он сравнивал колебания тела, вызванные гравитационным возмущением шара известной массы, и колебания, вызванные тяготением Земли. Он достаточно точно вычислил значение плотности Земли – 5,47 г/см3 (сегодня более точные расчеты дают 5,52 г/см3). Согласно различным источникам, значение гравитационной постоянной, высчитанное из гравитационного параметра с учетом плотности Земли, полученной Кавердишем, составило G=6,754·10−11 м³/(кг·с²), G = 6,71·10−11м³/(кг·с²) или G = (6,6 ± 0,04)·10−11м³/(кг·с²). До сих пор неизвестно, кто впервые получил численное значение постоянной Ньютона из работ Генри Кавердиша.

Измерение

Измерение силы тяжести Земли называется гравиметрией .

Спутниковые измерения

Карта гравитационных аномалий от GRACE

В настоящее время статические и изменяющиеся во времени параметры гравитационного поля Земли определяются с помощью современных спутниковых программ, таких как GOCE , CHAMP , Swarm , GRACE и GRACE-FO . Параметры с наименьшей степенью, включая сжатие Земли и движение геоцентра, лучше всего определяются с помощью спутниковой лазерной локации .

Крупномасштабные гравитационные аномалии могут быть обнаружены из космоса как побочный продукт спутниковых гравитационных миссий, например, GOCE . Эти спутниковые миссии направлены на восстановление детальной модели гравитационного поля Земли, обычно представленной в виде сферически-гармонического расширения гравитационного потенциала Земли, но альтернативные представления, такие как карты волн геоида или гравитационных аномалий, также являются произведено.

Гравитация восстановление и климат Эксперимент (GRACE) состоит из двух спутников , которые могут обнаружить гравитационные изменения по всей Земле. Также эти изменения могут быть представлены как временные вариации аномалии силы тяжести.

Искажения времени и пространства и черные дыры

Общая теория относительности Эйнштейна рассматривает гравитацию не как силу, а как искривление самого пространства вблизи массивного объекта. Согласно предсказаниям, свет, который традиционно следует по прямым линиям, искривляется при прохождении по искривленному пространству. Впервые это было продемонстрировано, когда астроном сэр Артур Эддингтон обнаружил изменение кажущегося положения звезды во время полного затмения в 1919 году, считая, что лучи света изгибаются под действием силы тяжести солнца.

Общая теория относительности также предсказывает, что если тело достаточно плотное, его сила тяжести исказит пространство настолько сильно, что свет вообще не сможет через него проходить. Такое тело поглощает свет и все остальное, что захватила его сильная гравитация, и носит название Черная дыра. Такое тело можно обнаружить только по его гравитационным эффектам на другие объекты, по сильному искривлению света вокруг него и по сильной радиации, излучаемой веществом, которое на него падает.

Все вещество внутри черной дыры сжато в центре, который имеет бесконечную плотность. «Размер» дыры определяется горизонтом событий, т.е. границей, которая окружает центр черной дыры, и ничто (даже свет) не может выйти за ее пределы. Радиус дыры называется радиусом Шварцшильда, в честь немецкого астронома Карла Шварцшильда (1873–1916), и вычисляется по формуле R_S = 2GM/c2, где c – это скорость света в вакууме. Если бы солнце попало в черную дыру, его радиус Шварцшильда составлял бы всего 3 км.

Существует надежное доказательство, что после того, как ядерное топливо массивной звезды иссякает, она больше не может противостоять коллапсу под своим собственным огромным весом и попадает в черную дыру. Считается, что черные дыры с массой в миллиарды солнц существуют в центрах галактик, включая нашу галактику, Млечный Путь. Многие ученые полагают, что суперяркие и очень отдаленные объекты под названием квазары, используют энергию, которая выделяется, когда вещество падает в черную дыру.

Согласно предсказаниям общей теории относительности, сила тяжести также искажает и время. Это также было подтверждено очень точными атомными часами, которые на уровне моря идут на несколько микросекунд медленнее, чем на территориях выше уровня моря, где сила тяжести Земли немного слабее. Вблизи горизонта событий это явление более заметно. Если наблюдать за часами астронавта, который приближается к горизонту событий, мы увидим, что часы идут медленнее. Находясь в горизонте событий, часы остановятся, но мы никогда не сможем этого увидеть. И наоборот, астронавт не заметит, что его часы идут медленнее, но он увидит, что наши часы идут быстрее и быстрее.

Основной опасностью для астронавта возле черной дыры были бы приливные силы, вызванные тем, что сила тяжести сильнее на тех частях тела, которые находятся ближе к черной дыре, чем на частях дальше от нее. По своей мощи приливные силы возле черной дыры, имеющей массу звезды, сильнее любого урагана и запросто разрывают на мелкие кусочки все, что им попадается. Однако, тогда как гравитационное притяжение уменьшается с квадратом расстояния (1/r2), приливно-отливное явление уменьшается с кубом расстояния (1/r3). Поэтому в отличие от принятого мнения, гравитационная сила (включая приливную силу) на горизонтах событий больших черных дыр слабее, чем на маленьких черных дырах. Так что приливные силы на горизонте событий черной дыры в наблюдаемом космосе, были бы менее заметны, чем самый мягкий ветерок.

Растяжение времени под действием силы тяжести вблизи горизонта событий является основой новой космологической модели физика-креациониста, доктора Рассела Хамфриса, о которой он рассказывает в своей книге «Свет звезд и время». Эта модель, возможно, помогает решить проблему того, как мы можем видеть свет отдаленных звезд в молодой вселенной. К тому же на сегодня она является научной альтернативой небиблейской теории «большого взрыва», которая основывается на философских предположениях, выходящих за рамки науки.

Гравитационное притяжение

Закон всемирного тяготения.

В рамках классической механики гравитационное притяжение описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы и , разделёнными расстоянием , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:

−11

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося также и при изучении излучений, и являющегося прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Гравитационное поле, так же как и поле силы тяжести, потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность гравитационного поля влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в гравитационном поле часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях, и все массы положительны, это, тем не менее, очень важная сила во Вселенной. В частности, электромагнитное взаимодействие между телами в космических масштабах мало, поскольку полный электрический заряд этих тел равен нулю (вещество в целом электрически нейтрально).

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. Аристотель (IV в. до н.э.) считал, что объекты с разной массой падают с разной скоростью. Только много позже (1589) Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Каково направление силы тяжести

Опыт. Если взять отвес или привязанный к нити какой-либо предмет (рис. 70), то увидим, что нить с грузиком вследствие действия на него силы тяжести всегда направлена к Земли вдоль прямой, которую называют вертикалью.

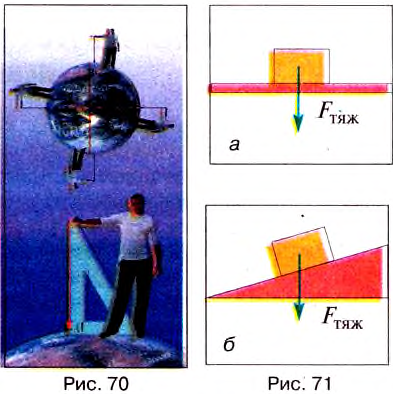
Выполнив этот опыт во всех точках Земли, учёные убедились, что сила тяжести всегда направлена к центру Земли.

Силу тяжести изображают в виде вертикальной стрелки, направленной вниз и приложенной к определённой точке тела (рис. 71 а, б).

Кстати:

Кроме планет с их спутниками вокруг Солнца двигаются малые планеты, которые еще называют астероидами. Наибольшая из них — Церера — имеет статус карликовой планеты и радиусом почти в 20 раз, а по массе в 7500 раз меньше Земли. Сила тяжести на ней настолько мала, что человек, оттолкнувшись от поверхности планеты, мог бы улететь с нее.

Вот как описывает основатель теории космонавтики К,Э. Циолковский в рассказе «Путь к звездам» условия пребывания человека на этом астероиде: «На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны. Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона».

Есть ли в космосе гравитация

Когда мы смотрим кино о космосе или видим трансляцию с МКС, в которой космонавты парят в невесомости, многие из нас думают, что там нет гравитации. Это ошибка.

На самом деле гравитация на орбите не то, что есть, она там почти ничем не отличается от той, что мы ощущаем на Земле. Если брать расстояние от центра Земли до МКС, то оно будет примерно на 10 процентов больше расстояния от центра Земли до ее поверхности. Если вспомнить, что гравитация зависит от размера тел и от их расстояния друг от друга, то становится понятно, что гравитация на орбите сильно меньше земной.

Космонавты могут ощущать невесомость не из-за того, что на орбите нет гравитации, а из-за того, что они постоянно находятся в состоянии свободного падения вместе со своим кораблем или космической станцией. Тем не менее, если поставить огромную стремянку и подняться на верхнюю ступеньку, которая будет на высоте орбиты МКС, мы не взлетим, а будем стоять на ней. Сила нашего притяжения немного изменится, но не настолько, чтобы взлететь.

Это не из-за отсутствия гравитации, а наоборот, из-за того, что она есть.

Если говорить совсем просто, космическая станция на орбите движется с огромной скоростью и постоянно стремится как бы пролететь мимо Земли. Ее гравитация в свою очередь удерживает станцию от ”улета”. В итоге, космонавты с их кораблем крутятся вокруг Земли и за счет центробежной силы находятся в уравновешенном состоянии невесомости. Получается, что гравитация на орбите есть и более того, именно она позволяет космонавтам испытывать невесомость, как бы парадоксально это не прозвучало.

Что такое гравитация простыми словами детям.

с лат. gravitas — «тяжесть» ) — невидимая сила , притягивающая объекты с меньшей массой к более массивным. Таким образом определяющая положение галактик, планет, спутников и всех небесных тел. В контексте Земли отвечает за то, что объекты притягиваются к поверхности и не улетают за пределы планеты. Это одно из четырех фундаментальных взаимодействий в физике, определяющих функционирование вселенной, наряду со слабым и сильным атомными взаимодействиями и электромагнетизмом.

Точного научного определения термина не существует, поскольку подходы к изучению гравитации и теории относительно её природы постоянно разрабатываются, дополняются и совершенствуются. Актуальными на сегодня являются закон всемирного тяготения Ньютона вместе с его дополнениями и общая теория относительности Эйнштейна.

Гравитация и закон всемирного тяготения

Закон всемирного тяготения, предложенный Ньютоном, не ставит своей целью описание природы возникновения гравитации, но позволяет совершать верные математические расчеты на практике. Для этого пользуются формулой

, где:

• F — сила притяжения;
• r — расстояние между их центрами;
• G — гравитационная постоянная, равная 6.67×10 -11 м 3 /кг×с 2 и отражающая то, с какой силой бы действовали друг на друга два тела, размещенные на расстоянии 1 метра и имеющие одинаковую массу в 1 килограмм.

Собственное гравитационное поле создается каждым объектом Вселенной вне зависимости от его массы.

Гравитация на каждой из планет разная и напрямую зависит от массы астрономического тела. Так, к примеру, показатели гравитации на Юпитере многократно превышают земные. На тело, имеющее земной вес в 60 килограмм, Юпитер будет оказывать такую гравитацию, как Земля оказывает на тело с массой 142 килограмма.

Гравитация и общая теория относительности

Несмотря на то, что закон всемирного тяготения Ньютона отлично справляется с математическим описанием гравитации, он порождает конфликты и несоответствия, когда речь заходит о дальности действия и скорости распространения этой величины.

Дело в том, что в теории Ньютона предполагается, что гравитация окутывает всю вселенную и действует мгновенно в каждой её части. Однако, это невозможно исходя из того, что пределом допустимой скорости в физике является скорость света. Даже если бы скорость распространения гравитации была равна скорости света, она бы не могла мгновенно срабатывать даже на небольших участках космоса, поскольку нуждается в преодолении расстояния.

Решение проблемы нашлось в общей теории относительности Эйнштейна, которая рассматривает гравитацию не как силу, но как искривление времени-пространства под влиянием масс.

Для наглядности можно представить натянутую вокруг обруча ткань. После того, как на нее положат яблоко, она искривится. Если же после этого положить рядом тяжелую гирю, она искривится уже с центром в новом месте , а яблоко притянет к гире.

В физике элементарных частиц была выработана концепция гравитона — гипотетически существующей фундаментальной частицы, которая ответственна за гравитацию. Такая частица имеет нулевую массу, однако, обладает энергией, позволяющей ей влиять на поведение других элементарных частиц.

Понятие гравитационных волн

Несмотря на то, что общая теория относительности Эйнштейна уже давно была принята научным сообществом, она нашла очередное свое подтверждение с открытием физиками гравитационных волн в 2015 году.

Людям, далеким от теоретической физики и астрономии, будет нетрудно представить гравитационные волны в виде кругов, некоторое время разрастающихся, а затем затухающих после того, как в воду был брошен камень. Они имеют относительно похожую форму и структуру, но проявляются не на поверхности воды, а в пространстве-времени Вселенной.

Гравитационные волны оказывают дополнительное влияние на все близлежащие объекты и возникают при резкой смене массы в конкретной точке. Примером такого изменения в структуре космоса может быть слияние сверхмассивных черных дыр.

Ученые не могли столь долго открыть такие волны из-за низкой силы гравитации. Даже при сегодняшнем уровне развития технологий для этого пришлось поместить в вакуум четырехкилометровый детектор , состоящий из подвешенных зеркал.

Людям ошибочно кажется, что гравитация невероятно сильна. На самом же деле, это самая слабая из всех фундаментальных взаимодействий. Иллюстрацией того, насколько сильно её превосходит, к примеру, электромагнитное взаимодействие может служить факт того, что даже маленькие магниты на холодильник надежно закреплены магнитным притяжением на своем месте и будто игнорируют силу земного притяжения.

Инерционная и гравитационная массы

Как уже отмечалось выше, Галилей был первым, кто наблюдал, что объекты падают на землю с одинаковой скоростью, независимо от их массы. В формулах Ньютона понятие массы происходит от двух разных уравнений. Второй его закон говорит, что сила F, приложенная к телу с массой m, дает ускорение по уравнению F = ma.

Однако сила тяжести F, приложенная к телу, удовлетворяет формуле F = mg, где g зависит от другого тела, взаимодействующего с рассматриваемым (земли обычно, когда мы говорим о силе тяжести). В обоих уравнений m есть коэффициент пропорциональности, но в первом случае это инерционная масса, а во втором – гравитационная, и нет никакой очевидной причины, что они должны быть одинаковыми для любого физического объекта.

Однако все эксперименты показывают, что это действительно так.

Проект «Изучение свободного падения»

При свободном падении на объекты воздействует только сила гравитации. Если мы бросим монету и перо с высоты 30 см, теоретически они должны падать с одинаковой скоростью и оказаться на земле одновременно. Всем известно, что монета упадёт гораздо раньше. Так почему же на оба объекта влияет одна и та же сила, и они приземляются не одновременно? Гравитация – это сила, которая тянет нас к земле. Для объектов в состоянии свободного падения эта сила равна ускорению, которое на земле составляет 9,8 м/с². Используя законы движения Ньютона, студенты продемонстрируют взаимосвязь между массой, силой и ускорением в процессе свободного падения.

Дети
выучат законы движения Ньютона,
продемонстрировав в результате опыта
взаимосвязь между массой, силой и
ускорением в процессе свободного
падения.

Что нам понадобится:

• трубка для изучения свободного падения / вакуумная трубка;
• монета;
• перо;
• клейкая лента;
• рулетка или сантиметровая лента;
• видеокамера и программа для редактирования видео (по желанию).

Ход эксперимента:

1. Отмерьте на стене 180 см от пола и отметьте через каждые 30 см кусочком клейкой ленты.
2. По желанию: включите видеокамеру для записи эксперимента. Установите камеру на высоте приблизительно 120 см от пола, чтобы она располагалась в одной плоскости с падающим объектом.
3. Возьмите монету и перо, бросьте их с высоты 90 см. Какой предмет упадёт первым?
4. Увеличивайте высоту на 30 см каждый раз. Что происходит со скоростью монеты и пера по мере увеличения высоты?
5. Установите трубку для свободного падения, поместите перо и монету в камеру. Запечатайте её и откачайте воздух из трубки, чтобы создать вакуум.
6. Поверните трубку так, чтобы перо и монета оказались в одном конце. Быстро разверните трубку на 180°, чтобы монеты и перо упали в другой конец трубки. Какой предмет окажется в другом конце первым?
7. Если вы записывали эксперимент на видео, подсчитайте скорость (м/с). Для этого, используя программу для редактирования видео, посмотрите его в замедленном варианте. Используйте отметки на стене и часы или таймер, чтобы определить скорость падения предметов с разной высоты, а также внутри трубки.

Теория гравитации Эйнштейна

Он взял факт равенства инерционной и гравитационной масс как отправную точку для своей теории. Ему удалось построить уравнения гравитационного поля, знаменитые уравнения Эйнштейна, и с их помощью вычислить правильное значение для прецессии орбиты Меркурия. Они также дают измеренное значение отклонения световых лучей, которые проходят вблизи Солнца, и нет никаких сомнений в том, что из них следуют правильные результаты для макроскопической гравитации. Теория гравитации Эйнштейна, или общая теория относительности (ОТО), как он сам ее назвал, является одним из величайших триумфов современной науки.

Проект «Зависимость времени падения от высоты»

Физика утверждает, что свободное падение происходит тогда, когда единственная сила, воздействующая на объект, — это гравитация. Учитывая, что ускорение свободного падения на земле постоянно, расстояние падения объекта пропорционально времени падения. В этом эксперименте вы сможете определить ускорение свободного падения, а также протестировать ваше собственное время реагирования. Время реагирования – это время, которое требуется вам для того, чтобы отреагировать на какое-либо событие: в данном случае, падение метровой линейки или денежной купюры. Быстрее ли ваша реакция, чем ускорение свободного падения.

Ход эксперимента:

1. Пусть ваш
   друг возьмет в руки линейку, так чтобы
   сторона, на которой отмечен «0», находилась
   сразу над вашей рукой.
2. Он должен
   включить таймер сразу после того, как
   выпустит из рук линейку и остановить
   таймер сразу, когда вы её поймаете.
3. Запишите
   расстояние и время.
4. Повторите
   несколько раз, бросая линейку с разной
   высоты. Как взаимосвязаны время и
   расстояние, пройденное предметом?
5. Запишите
   результаты, постройте график. Время
   будет отмечено на оси x, а расстояние,
   пройденное предметом, будет отмечаться
   на оси y.
6. Используйте
   следующее уравнение, чтобы подсчитать
   время, которое потребуется для того,
   чтобы линейка упала. Насколько близки
   ваши результаты и показатели секундомера?

d=g*t2/2,

где d – это расстояние, пройденное объектом, в метрах,g – ускорение свободного падения,t– время в секундах.

1. Рассчитайте
   ускорение в каждом пункте графика.
   Насколько оно совпадает с ускорением
   свободного падения на Земле?

a=2d/t2.

1. Повторите
   эксперимент с денежной купюрой.
   Используйте вышеупомянутое уравнение,
   чтобы подсчитать, сколько времени
   понадобится для того, чтобы купюра
   прошла через ваши пальцы по всей длине.
   Сможете ли вы поймать её?

Вывод:

Падают
ли все объекты с одинаковой скоростью?
Имеет ли значение вес объекта для
скорости падения тела?
Как связаны расстояние и время свободного
падения объектов? Как определить силу
свободного падения?

График
результатов показывает, что проделанное
расстояние пропорционально квадрату
времени, затраченному в процессе падения.
В результате расчётов ускорения вы
должны получить примерно 9,81 м/с². Время
реагирования человека составляет
приблизительно 0,25 секунды,
что для большинства людей не достаточно
быстро, чтобы успеть ухватить купюру.
Почему? График, который вы построили,
покажет, что чем дольше падает линейка,
тем быстрее она прекращает движение.
Это объясняет кривая на графике: из-за
постоянного ускорения, вызванного силой
гравитации, скорость объекта будет
расти быстрее.

При
свободном падении ускорение всех тел
одинаково, этот факт объясняется тем,
что сила тяжести пропорциональна
массе Земли. Также, при этом, сила
гравитации Земли, тянущая вниз, и
сила сопротивления воздуха, подталкивающая
вверх, равны. Хорошей аналогией будет
полет парашютиста:
несмотря на то, что гравитация всё ещё
действует на его тело, скорость
его падения не настолько
большая, поскольку сила воздуха
поддерживает его. В этом эксперименте
сопротивление воздуха и торможение не
являются главным вопросом, поскольку
объекты падают на очень короткие
расстояния.

Физический механизм гравитации

Ньютон был не полностью удовлетворен своей теорией, поскольку она предполагала взаимодействие между притягивающимися телами на расстоянии. Сам великий англичанин был уверен, что должен существовать некий физический агент, ответственный за передачу действия одного тела на другое, о чем он вполне ясно высказался в одном из своих писем. Но время, когда было введено понятие гравитационного поля, которое пронизывает все пространство, наступило лишь через четыре столетия. Сегодня, говоря о гравитации, мы можем говорить о взаимодействии любого (космического) тела с гравитационным полем других тел, мерой которого и служат возникающие между каждой парой тел гравитационные силы. Закон всемирного тяготения, сформулированный Ньютоном в вышеприведенной форме, остается верным и подтверждается множеством фактов.

Закон всемирного тяготения. Формулы

В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1.10.1. Шаровидное тело имеет центр массы, совпадающий с центром шара.

Рисунок 1.10.1. Гравитационные силы притяжения между телами. F1→=-F2→.

Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.

Определение 1

При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.

Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.

От астрономических таблиц до закона Всемирного тяготения

Одними из самых серьезных научных результатов, полученных в то время, были астрономические таблицы Тихо Браге (1546 — 1601). Данные таблицы были одними из самых точных астрономических таблиц, полученных к тому времени. На основе них, ученик Тихо Браге — Иоганн Кеплер (1571 — 1630) получил самые известные законы астрономии — Законы Кеплера. Основные идеи Кеплер подчерпнул в написанных ранее работах. Так, он пользовался идеями гелиоцентричности солнечной системы и предположении о том что сила гравитационного взаимодействия убывает обратно пропорционально расстоянию между телами.

Анализ астрономических таблиц

Кеплер получил свои законы на основе анализа реальных данных. Он пытался найти общий закон, который бы позволил описать движение любых космических тел, но не смог получить общего правила. Несмотря на это, Кеплер впервые высказал почти все идеи, которые использовал позже Ньютон. Хотя законы Кеплера и были получены эмпирически, последующие проверки астрономами-теоретиками показали, что они абсолютно справедливы для Солнечной системы.

Однако работы Кеплера не носили только лишь описательный характер. На основе анализа движения 6 известных на то время планет в Солнечной системе он высказал предположение о наличие других планет, вносящих коррективы в орбиты. Также Кеплер попытался связать явление прилива и отлива с движением Луны и ее гравитационным взаимодействием с Землей.

Законы Кеплера

1 Закон Кеплера

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

2 Закон Кеплера

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает собой равные площади.

Равенство площадей, описанных радиус-вектором от Солнца к планете за равные промежутки времени

3 Закон Кеплера

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.

$$\frac{T_{1}^{2}}{T_{2}^{2}} = \frac{a_{1}^{3}}{a_{2}^{3}}$$

Чуть позже, Исаак Ньютон (1642 — 1727) уточнил третий закон:

$$\frac{T_{1}^{2}\left(M + m_{1}\right)}{T_{2}^{2}\left(M + m_{2}\right)} = \frac{a_{1}^{3}}{a_{2}^{3}}$$

где \(M\) — масса Солнца, \(m_{1}\) и \(m_{2}\) — массы планет.

\(F_0, F_1\) — фокусы эллипса для планеты \(P_1\), а \(F_0, F_2\) — для планеты \(P_2\)

Закон Всемирного Тяготения

После работ Иоганна Кеплера наука очень сильно продвинулась в объяснении гравитационного взаимодействия, но продвижение было весьма специфическим. Учены могли скорее ответить на вопрос «Что наблюдается?» вместо желаемого «Почему наблюдается именно это?».

Ответить на второй вопрос решился Исаак Ньютон. Объединив все известные на тот момент качественные описания, работы Иоганна Кеплера и рассмотрев еще несколько предположений, Ньютон получил, пожалуй, один из самых известных законов природы — Закон Всемирного Тяготения:

$$F = \frac{GMm}{R^{2}}$$

где \(F\) — сила гравитационного притяжения, \(M\) и \(m\) — массы притягивающихся тел, \(R\) — расстояние между взаимодействующими телами, \(G = 6.67 \cdot 10^{-11} \frac{\text{м}^{2}\cdot \text{Н}}{\text{кг}^{2}}\) — гравитационная постоянная.

Важность результатов, полученных Ньютоном, трудно переоценить. Помимо строгой математической формулировки Закона Всемирного Тяготения Исаак Ньютон предоставил научному сообществу целую математическую модель, в которой данный закон применим для всех тел, обладающих ненулевой массой

Также благодаря Ньютону появились основы интегрального и дифференциального исчисления (Изложенные в математических основах натуральной философии).

Возмущение в движении планет

Законы Кеплера, описывающие траектории движения планет, учитывают только тяготение Солнца и упускают влияние других объектов системы. Поэтому при реальных наблюдениях за вращением какого-либо небесного тела можно увидеть небольшие отклонения от предсказанной орбиты, нехарактерные для кеплеровских постулатов. Эти отклонения называют возмущениями, и в сегодняшней науке рассчитываются достаточно точно благодаря формуле тяготения и известным значениям расстояний между Солнцем и планетами, а также их масс.

Нептун

Одно из самых масштабных проявлений возмущений в науке – несоответствие рассчитанного и наблюдаемого движения планеты Уран, открытой Вильямом Гершелем в 1781 году. Несмотря на то, что было учтено влияние как звезды, так и остальных тел, существовали небольшие отклонения, с которыми астрономы никак не могли примириться. Тогда было высказано предположение о существовании за Ураном ещё одной, восьмой планеты. В 1846 году на основании расчетов Урбена Леверье и Джона Адамса она была найдена, получив название Нептун. А в 1930 году подобным образом, «на кончике пера», открылось существование Плутона, споры о статусе которого не утихают и по сей день.